numerical-methods程序代写
numerical-methods-montecarlointegrati
on-exercise
In this exercise, you should implement classes that provide a reasonably flexible
framework for Monte-Carlo integration.
The framework should be flexible enough to allow
• integration of different functions f : Rn → R
• flexible specification of the integration domains using a transformation from
[0,1]n to a subset of Rn
• flexible use for different random number generators
For convenience, we provide the interfaces that define the framework. You can find
these interfaces in the package
info.quantlab.numericalmethods.lecture.montecarlo.integration
Interfaces (provided)
• Integrand
• IntegrationDomain
• Integrator
• MonteCarloIntegratorFactory
The MonteCarloIntegratorFactory's method requires a class implementing
a RandomNumberGenerator. This interface and some classes implementing this interface can
be found in the package
info.quantlab.numericalmethods.lecture.randomnumbers
Integrand and IntegrationDomain
• Objects implementing Integrand provide a function f : A
ightarrow R defined on a domain
A.
• Objects implementing IntegrationDomain provide a bijective function g : [0,1]^{n}
ightarrow
A that transforms the integration domain and the determinant of the derivative (Jacobi matrix)
dg/dx.
• Objects implementing Integrator provide the integral int_A f(z) dz using substitution z =
f(x).
Classes
You may use the classes providing random number generators that will be or were
developed during the lecture, e.g.,
• RandomNumberGeneratorFrom1D
• MersenneTwister
Task
The exercise consists of two separate tasks.
Task 1: A MonteCarloIntegrator
To complete your task:
•
i. Implement a class implementing the interface Integrator that performs a general
Monte-Carlo integration of arbitrary functions on general domains.
The function to integrate will be provided to the integrator's method integrate as an
object implementing the interface Integrand.
The integration domain will be provided to the integrator's method integrate as an
object implementing the interface IntegrationDomain.
•
ii. Implement a class implementing the interface MonteCarloIntegratorFactory that
allows creating an object of the class that you have implemented in 1). Note:
the MonteCarloIntegratorFactory simply calls the constructor of your class.
•
ii. To allow us to test you implementation, complete the implementation of the
method getMonteCarloIntegratorFactory of MonteCarloIntegrationAssignmentSolutio
n. This allows the creation of an object of your MonteCarloIntegratorFactory. Our unit
tests will use this to test your code.
•
ii. Feel free to create your own UnitTests and JavaDoc documentation.
Suggestion: you may test your integrator with different random number generators,
e.g. MersenneTwister via
final long seed = 3141;
RandomNumberGenerator randomNumberGenerator = new RandomNumberGeneratorFrom1D(new
MersenneTwister(seed), domain.getDimension());
or a HaltonSequence.
Task 2: Using your MonteCarloIntegrator to calculate the integral
of a DoubleBinaryFunction
•
v. Complete the method getIntegral of MonteCarloIntegrationAssignmentSolution. Use
your Monte-Carlo integrator with approximately 1 million sample points to calculate
the integral.
Tasks 3: Implement a SimpsonsIntegrator for the general
Simpson's rule in d dimension
To complete your task:
•
vi. Implement a class implementing the interface Integrator that performs a general
(composite) Simpson's rule integration in d dimension of arbitrary functions on
general domains.
The function to integrate will be provided to the integrator's method integrate as an
object implementing the interface Integrand.
The integration domain will be provided to the integrator's method integrate as an
object implementing the interface IntegrationDomain.
•
vii. Implement a class implementing the interface IntegratorFactory that allows creating
an object of the class that you have implemented in 1). Note:
the IntegratorFactory simply calls the constructor of your class.
•
vii. To allow us to test you implementation, complete the implementation of the
method getSimpsonsIntegratorFactory of MonteCarloIntegrationAssignment. This
allows the creation of an object of your IntegratorFactory. Our unit tests will use this
to test your code.
•
vii. Feel free to create your own UnitTests and JavaDoc documentation.
Hints
• Note that your Simpsons integral and your Monte-Carlo integral only operator
on [0,1]^d (the object implementing the Domain will provide you with the
transformation).
• Your Simpsons integrator should accept the numberOfValuationPoints as an
argument. This should be the minimum total number of valuation points. Since
the Simpsons rule uses an odd number of points in every dimension, you may
use the following code to round this number appropriately
to numberOfSamplePointsEffective, using numberOfSamplePointsPerDimension per
dimension.
int dimension = integrationDomain.getDimension();
int numberOfValuationPointsPerDimension = 2 * (int)
(Math.ceil(Math.pow(numberOfValuationPoints, 1.0/dimension))/2) + 1;
int numberOfValuationPointsEffective = (int)
Math.pow(numberOfValuationPointsPerDimension, dimension);
• You might realise that you need to think a bit to find a short algorithm to implement the
Simpsons integration in arbitrary dimensions. It is possible to create a fairly short
implementation if you implement a multi-index index - an array of length dimension where
each entry runs from 0 to numberOfSamplePointsPerDimension-1.
Unit Tests
We encourage you to write your own unit tests.
Further Research
This project offers the opportunity to explore Monte-Carlo integration in more detail for
those interested. Here are a few suggestions:
• Explore the dependency on the dimension: Consider the integration of x →
product(i=0,...,d-1) sin(xi) for 0 < xi < π. The value of the integral is 2^d. This is an
d-dimensional integral. For this function, compare the accuracy of Monte-Carlo
integration and Simpsons integration with d = 1, 2, 4, 8 using for example n =
5^8 = 390625 sample points.
• Explore the dependency on the smoothness of the function: Consider the
integration of (x0,x1) → x0
2 + x1
2 < 1.0 ? 1.0 : 0.0 for 0 < xi < 1. The analytic value of
this integral π. For this function, compare the accuracy of Monte-Carlo
integration and Simpsons integration using n = 101^2 = 10201 sample points.
请加QQ:99515681 邮箱:99515681@qq.com WX:codinghelp
- 眼内注药主要适用哪些眼病患者?北京爱尔英智眼科医院院长谷威为您讲解
- Line协议号注册器市场巅峰:我的LINE营销工具心得,让你事业一飞冲天
- 威雅学校直播预告:对话阿斯顿·马丁首席创意官
- Ins/Instagram自动创新营销软件,ins一键解锁引流新方法!
- Ins/IG群发营销助手大揭秘!Instagram暴力批量私信软件推荐!
- 法律GPT技术进一步提升律师工作效率,AlphaGPT赋能合同审查
- 华北建材:铸就品质,筑梦未来
- 科技大神揭秘:Telegram代拉群营销工具的超能力真实可信,绝对值得一试
- 代写Strategy Pattern for Abstract Data
- Instagram营销群发软件,Ins引流工具,让你的营销事半功倍!
- Ins/Instagram自动创新营销软件,ins一键解锁引流新方法!
- Instagram群发私信推广软件,ins自动发帖工具,ig群发黑科技
- CE-Channel: Choose Us for Easy Access to Global Partnerships, Opening the Doors to Overseas Markets
- Instagram自动吸粉引流神器,Ins全新营销工具现已推出!
- Instagram私信博主 - ins自动登录/ig采集指定地区/ins群发软件
- 网络通信革新:Telegram协议号如何提高通信效率?
- Instagram群发私信工具,ins营销软件,ig采集神器
- Instagram批量养号 - ins自动登录/ig采集指定地区/ins群发软件/批量群发
- FMS6303MTC1406X: Redefining Signal Conditioning for High-Performance Multimedia Systems | ChispX
- Ins群发脚本助手,Instagram一键群发工具,让你打造营销新格局!
- Instagram批量养号工具,Ins自动登录软件,ig群发营销软件
- Instagram自动登录 - ins群发工具/ig营销助手/ins引流神器/ig吸粉工具
- Ins自动登录软件,Ig采集指定地区工具,instagram营销引流
- 破格创新 吸引眼球 WhatsApp拉群营销工具带来新招数 让你的消息独领风骚 引爆市场
- TG群发加速器,电报智能营销软件,Telegram自助采集群发平台
- 看似普通的WhatsApp拉群工具 却为我的事业带来了不平凡的变革
- TG/Telegram如何群发,电报群发工具购买/TG协议号群发推荐
- 代写Algorithm for GCD
- 电报精准采集,高效营销!Telegram群发引流神器带你领跑!
- COMP284 代做、Java 语言编程代写
推荐
-
 疫情期间 这个品牌实现了疯狂扩张
记得第一次喝瑞幸,还是2017年底去北京出差的
科技
疫情期间 这个品牌实现了疯狂扩张
记得第一次喝瑞幸,还是2017年底去北京出差的
科技
-
 创意驱动增长,Adobe护城河够深吗?
Adobe通过其Creative Cloud订阅捆绑包具有
科技
创意驱动增长,Adobe护城河够深吗?
Adobe通过其Creative Cloud订阅捆绑包具有
科技
-
 升级的脉脉,正在以招聘业务铺开商业化版图
长久以来,求职信息流不对称、单向的信息传递
科技
升级的脉脉,正在以招聘业务铺开商业化版图
长久以来,求职信息流不对称、单向的信息传递
科技
-
 丰田章男称未来依然需要内燃机 已经启动电动机新项目
尽管电动车在全球范围内持续崛起,但丰田章男
科技
丰田章男称未来依然需要内燃机 已经启动电动机新项目
尽管电动车在全球范围内持续崛起,但丰田章男
科技
-
 如何经营一家好企业,需要具备什么要素特点
我们大多数人刚开始创办一家企业都遇到经营
科技
如何经营一家好企业,需要具备什么要素特点
我们大多数人刚开始创办一家企业都遇到经营
科技
-
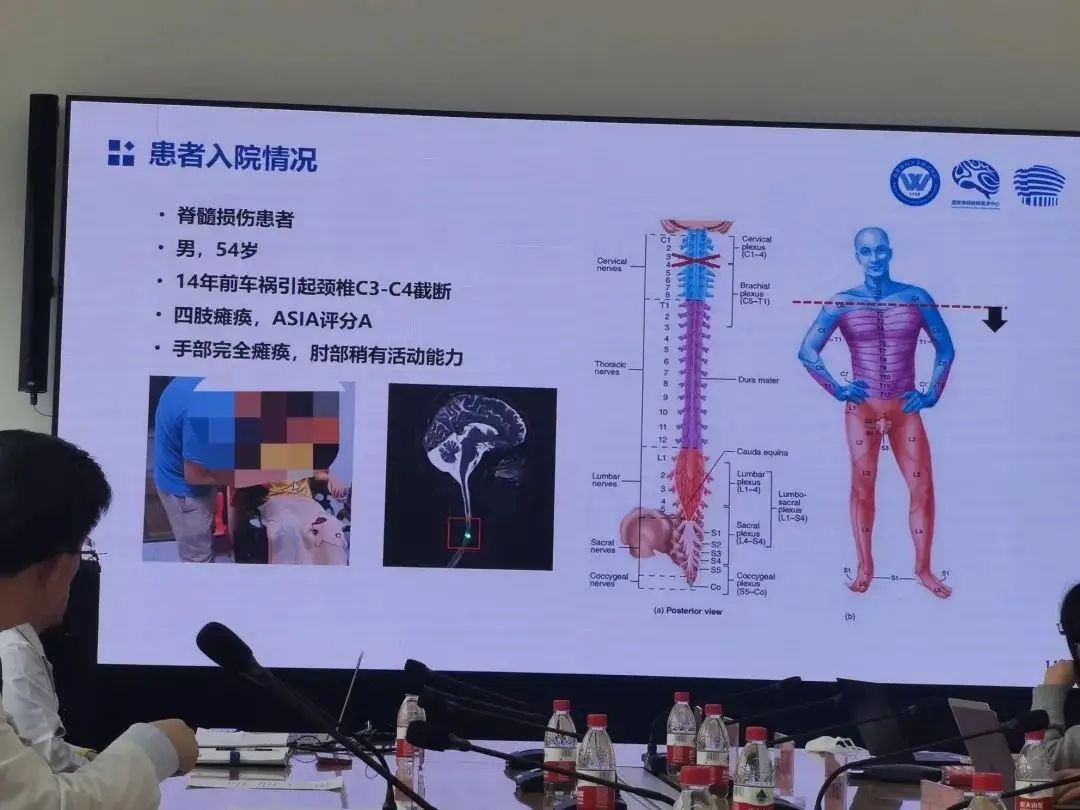 老杨第一次再度抓握住一瓶水,他由此产生了新的憧憬
瘫痪十四年后,老杨第一次再度抓握住一瓶水,他
科技
老杨第一次再度抓握住一瓶水,他由此产生了新的憧憬
瘫痪十四年后,老杨第一次再度抓握住一瓶水,他
科技
-
 全力打造中国“创业之都”名片,第十届中国创业者大会将在郑州召开
北京创业科创科技中心主办的第十届中国创业
科技
全力打造中国“创业之都”名片,第十届中国创业者大会将在郑州召开
北京创业科创科技中心主办的第十届中国创业
科技
-
 B站更新决策机构名单:共有 29 名掌权管理者,包括陈睿、徐逸、李旎、樊欣等人
1 月 15 日消息,据界面新闻,B站上周发布内部
科技
B站更新决策机构名单:共有 29 名掌权管理者,包括陈睿、徐逸、李旎、樊欣等人
1 月 15 日消息,据界面新闻,B站上周发布内部
科技
-
 苹果罕见大降价,华为的压力给到了?
1、苹果官网罕见大降价冲上热搜。原因是苹
科技
苹果罕见大降价,华为的压力给到了?
1、苹果官网罕见大降价冲上热搜。原因是苹
科技
-
 智慧驱动 共创未来| 东芝硬盘创新数据存储技术
为期三天的第五届中国(昆明)南亚社会公共安
科技
智慧驱动 共创未来| 东芝硬盘创新数据存储技术
为期三天的第五届中国(昆明)南亚社会公共安
科技

