代做Data 102
Data 102, Spring 2024
Homework 5
Due: 5:00 PM Friday, April 12, 2024
Submission Instructions
Homework assignments throughout the course will have a written portion and a code portion.
Please follow the directions below to properly submit both portions.
Written Portion:
• Every answer should contain a calculation or reasoning.
• You may write the written portions on paper or in LATEX.
• If you type your written responses, please make sure to put it in a markdown cell instead
of writing it as a comment in a code cell.
• Please start each question on a new page.
• It is your responsibility to check that work on all the scanned pages is legible.
Code Portion:
• You should append any code you wrote in the PDF you submit. You can either do so
by copy and paste the code into a text file or convert your Jupyter Notebook to PDF.
• Run your notebook and make sure you print out your outputs from running the code.
• It is your responsibility to check that your code and answers show up in the PDF file.
Submitting:
You will submit a PDF file to Gradescope containing all the work you want graded (including
your math and code).
• When downloading your Jupyter Notebook, make sure you go to File → Save and
Export Notebook As → PDF; do not just print page from your web browser because
your code and written responses will be cut off.
• Combine the PDFs from the written and code portions into one PDF. Here is a useful
tool for doing so. As a Berkeley student, you get free access to Adobe Acrobat, which
you can use to merge as many PDFs as you want.
• Please see this guide for how to submit your PDF on Gradescope. In particular, for
each question on the assignment, please make sure you understand how to select the
corresponding page(s) that contain your solution (see item 2 on the last page).
1
Data 102 Homework 5 Due: 5:00 PM PT Friday, April 12, 2024
Late assignments will count towards your slip days; it is your responsibility to ensure you
have enough time to submit your work.
Data science is a collaborative activity. While you may talk with others about the homework, please write up your solutions individually. If you discuss the homework with your
peers, please include their names on your submission. Please make sure any handwritten
answers are legible, as we may deduct points otherwise.
Simulation Study of Bandit Algorithms
In this problem, we evaluate the performance of two algorithms for the multi-armed bandit
problem. The general protocol for the multi-armed bandit problem with K arms and n rounds
is as follows: in each round t = 1, . . . , n the algorithm chooses an arm At ∈ {1, . . . , K} and
then observes reward Xt for the chosen arm. The bandit algorithm specifies how to choose
the arm At based on what rewards have been observed so far. In this problem, we consider
a multi-armed bandit for K = 2 arms, n = 50 rounds, and where the reward at time t is
Xt ∼ N (At − 1, 1), i.e. N (0, 1) for arm 1 and N (1, 1) for arm 2.
(a) (4 points) Consider the multi-armed bandit where the arm At ∈ {1, 2} is chosen according to the explore-then-commit algorithm (below) with c = 4. Let Gn =
Pn
t=1 Xt denote
the total reward after n = 50 iterations. Simulate the random variable Gn a total of
B = 2000 times and save the values G
(b)
n , b = 1, . . . , B in a list. Report the empirical
averaged regret 1
B
PB
b=1
50µ
∗ − G
(b)
n
(where µ
∗
is the mean of the best arm) and plot
a normalized histogram of the rewards.
Algorithm 1 Explore-then-Commit Algorithm
input: Number of initial pulls c per arm
for t = 1, . . . , cK : do
Choose arm At = (t mod K) + 1
end
Let Aˆ ∈ {1, . . . , K} denote the arm with the highest average reward so far.
for t = cK + 1, cK + 2, . . . , n : do
Choose arm At = Aˆ
end
(b) (4 points) Consider the multi-armed bandit where the arm At ∈ {1, 2} is chosen according to the UCB algorithm (below) with c = 4, n = 50 rounds. Repeat the simulation
in Part (a) using the UCB algorithm, again reporting the empirical averaged regret and
the histogram of G
(b)
n for b = 1 . . . B for B = 2000. How does the empirical averaged
regret compare to your results from part (a)?
Note: If TA(t) denote the number of times arm A has been chosen (up to and including
time t) and ˆµA,t is the average reward from choosing arm A (up to and including t), then
use the upper confidence bound ˆµA,TA(t−1) +
q2 log(20)
TA(t−1) . Note also that this algorithm
is slightly different than the one used in the lab and lecture as we are using an initial
exploration phase.
2
Data 102 Homework 5 Due: 5:00 PM PT Friday, April 12, 2024
Algorithm 2 UCB Algorithm
input: Number of initial pulls c per arm
for t = 1, . . . , cK : do
Choose arm At = (t mod K) + 1
end
for t = cK + 1, cK + 2 . . . : do
Choose arm At with the highest upper confidence bound so far.
end
(c) (1 point) Compare the distributions of the rewards by also plotting them on the same
plot and briefly justify the salient differences.
Markov Decision Process for Robot Soccer
A soccer robot R is on a fast break toward the goal, starting in position 1. From positions
1 through 3, it can either shoot (S) or dribble the ball forward (D). From 4 it can only shoot.
If it shoots, it either scores a goal (state G) or misses (state M). If it dribbles, it either
advances a square or loses the ball, ending up in state M.
In this Markov Decision Process (MDP), the states are 1, 2, 3, 4, G, and M, where G
and M are terminal states. The transition model depends on the parameter y, which is the
probability of dribbling successfully (i.e., advancing a square). Assume a discount of γ = 1.
For k ∈ {1, 2, 3, 4}, we have
Pr(G | k, S) = k
6
Pr(M | k, S) = 1 −
k
6
Pr(k + 1 | k, D) = y
Pr(M | k, D) = 1 − y,
R(k, S, G) = 1
and rewards are 0 for all other transitions.
(a) (3 points) Denote by V
π
the value function for the specific policy π. What is V
π
(1) for
the policy π that always shoots?
(b) (4 points) Denote by Q∗
(s, a) the value of a q-state (s, a), which is the expected utility
when starting with action a at state s, and thereafter acting optimally. What is Q∗
(3, D)
in terms of y?
(c) (3 points) For what range of values of y is Q∗
(3, S) ≥ Q∗
(3, D)? Interpret your answer
in plain English.
请加QQ:99515681 邮箱:99515681@qq.com WX:codinghelp
- WhatsApp全球拉群,ws协议号自动注册工具/ws群发/ws养号
- “广进计划”能实现“降本增效”吗?
- WhatsApp协议注册软件/ws群发/ws营销工具/ws业务咨询大轩
- Ins引流营销助手,Instagram拉群群发软件,助你快速壮大粉丝团!
- Telegram一键自动定位采集营销助手,TG全球坐标定位采集软件
- CS 211编程代做、代写c/c++,Java程序
- InBody体成分系列产品荣获欧盟CE-MDR认证 加速全球布局步伐
- 碧桂园服务:以进促稳,年收入增长至人民币约426.1亿元
- 忆联再次以第一成交候选人入围中国移动SSD硬盘AVAP项目
- 曾经的我为了推进工作焦头烂额但现在 有了WhatsApp拉群工具 一键发送的利器 我轻轻松松推进事业 简直是事业的指南针
- 微软电脑管家发布2周年:携手用户,共创价值
- Ins群发脚本助手,Instagram群发拉群营销软件,让你打造营销新格局!
- 全方位Telegram代群发,助力品牌全球曝光
- 掌握商业风向WhatsApp工具教你如何时刻关注趋势成就无限商机
- instagram深度推广引流营销软件,ins自动化群发助手
- 创意传媒巨星 WhatsApp拉群工具助你打造独特营销手法 让消息成为关注焦点
- WhatsApp拉群的步骤是什么
- 微型泵领域的创新小先锋-记威尔特(广州)流体设备
- ins超好用群发神器!Instagram自动采集博主粉丝,Ins营销必备工具!
- WhatsApp群发如何避免封控/ws协议号/ws云控/ws注册
- 代写CSCI 2122、C++编程设计代做
- Instagram精准私信群发营销神器,Ins引流推广最新软件购买!
- 热辣滚烫!2024低代码6大趋势
- Instagram引流营销助手,Ins拉群软件,共同助你实现营销目标!
- Instagram营销采集软件,ins超强采集私信工具/ig采集神器来袭
- 国美金融集中发力AI:多维度智能风控,全面推进数字化转型升级
- 世贸通美国移民EB5投资移民:每年超100万人选择移民美国
- ins群发软件好用吗?Instagram独家引流推广群发软件,博主推荐购买!
- tg群发助手,tg营销群发软件,神器帮助你迅速获客
- Instagram营销群发工具,ins私信采集软件/ig博主采集神器/测试联系大轩
推荐
-
 全力打造中国“创业之都”名片,第十届中国创业者大会将在郑州召开
北京创业科创科技中心主办的第十届中国创业
科技
全力打造中国“创业之都”名片,第十届中国创业者大会将在郑州召开
北京创业科创科技中心主办的第十届中国创业
科技
-
 疫情期间 这个品牌实现了疯狂扩张
记得第一次喝瑞幸,还是2017年底去北京出差的
科技
疫情期间 这个品牌实现了疯狂扩张
记得第一次喝瑞幸,还是2017年底去北京出差的
科技
-
 创意驱动增长,Adobe护城河够深吗?
Adobe通过其Creative Cloud订阅捆绑包具有
科技
创意驱动增长,Adobe护城河够深吗?
Adobe通过其Creative Cloud订阅捆绑包具有
科技
-
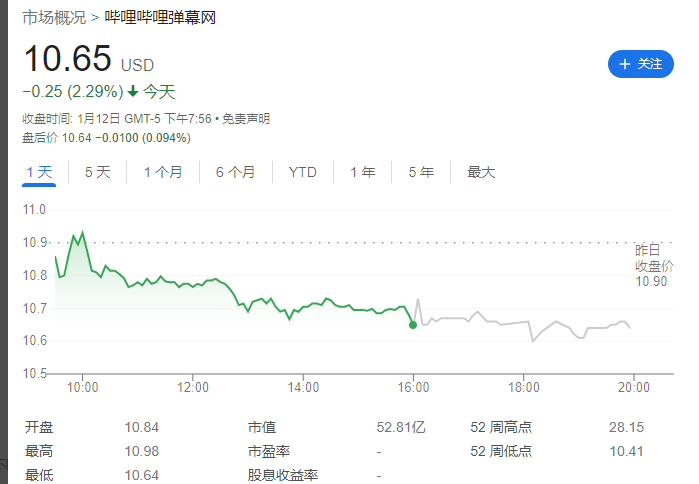 B站更新决策机构名单:共有 29 名掌权管理者,包括陈睿、徐逸、李旎、樊欣等人
1 月 15 日消息,据界面新闻,B站上周发布内部
科技
B站更新决策机构名单:共有 29 名掌权管理者,包括陈睿、徐逸、李旎、樊欣等人
1 月 15 日消息,据界面新闻,B站上周发布内部
科技
-
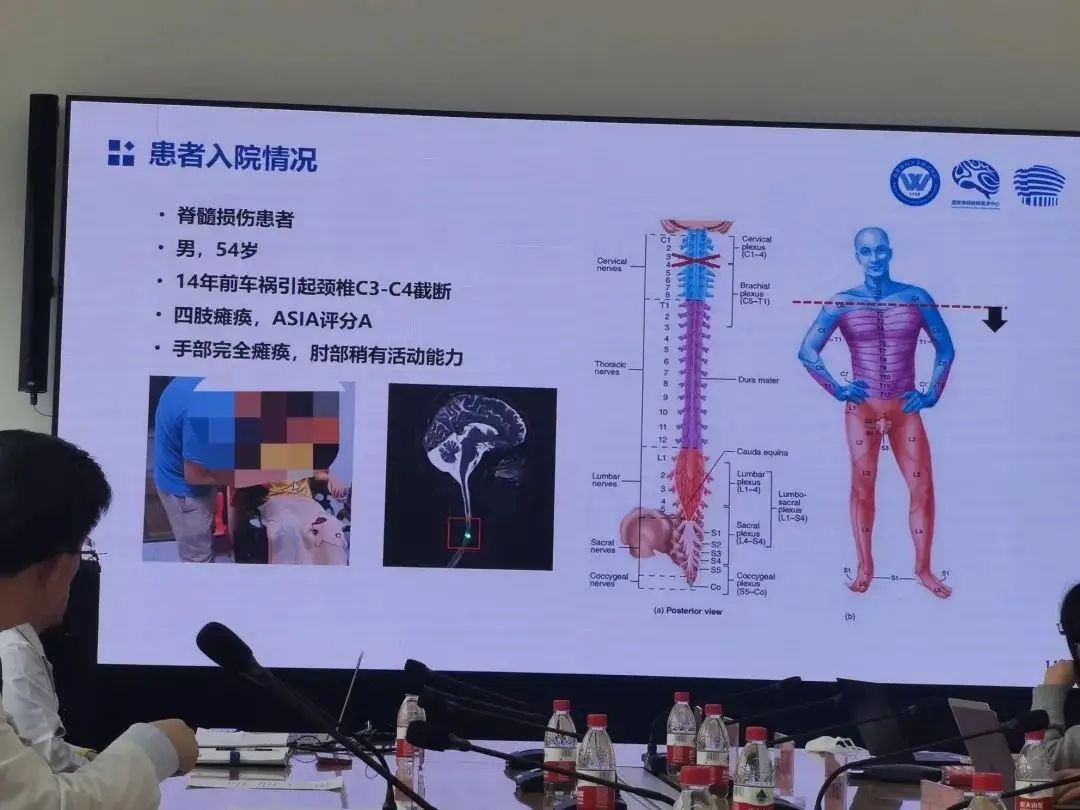 老杨第一次再度抓握住一瓶水,他由此产生了新的憧憬
瘫痪十四年后,老杨第一次再度抓握住一瓶水,他
科技
老杨第一次再度抓握住一瓶水,他由此产生了新的憧憬
瘫痪十四年后,老杨第一次再度抓握住一瓶水,他
科技
-
 智慧驱动 共创未来| 东芝硬盘创新数据存储技术
为期三天的第五届中国(昆明)南亚社会公共安
科技
智慧驱动 共创未来| 东芝硬盘创新数据存储技术
为期三天的第五届中国(昆明)南亚社会公共安
科技
-
 苹果罕见大降价,华为的压力给到了?
1、苹果官网罕见大降价冲上热搜。原因是苹
科技
苹果罕见大降价,华为的压力给到了?
1、苹果官网罕见大降价冲上热搜。原因是苹
科技
-
 如何经营一家好企业,需要具备什么要素特点
我们大多数人刚开始创办一家企业都遇到经营
科技
如何经营一家好企业,需要具备什么要素特点
我们大多数人刚开始创办一家企业都遇到经营
科技
-
 丰田章男称未来依然需要内燃机 已经启动电动机新项目
尽管电动车在全球范围内持续崛起,但丰田章男
科技
丰田章男称未来依然需要内燃机 已经启动电动机新项目
尽管电动车在全球范围内持续崛起,但丰田章男
科技
-
 升级的脉脉,正在以招聘业务铺开商业化版图
长久以来,求职信息流不对称、单向的信息传递
科技
升级的脉脉,正在以招聘业务铺开商业化版图
长久以来,求职信息流不对称、单向的信息传递
科技

